\[ \newcommand\si[1]{\mathrm{#1}} \newcommand\SI[2]{#1\,\si{#2}} \newcommand\matr[1]{\mathbf{#1}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \]
Global positioning systems
1 How is a global positioning system (GPS) used in civil applications?
Land, sea, air, and space navigation
Intelligent Vehicle Highway System (IVHS)
Search and rescue
Mapping and GIS
Recreation
Surveying
2 Three main components of GPS
Space segment: GPS satellites
Control segment: Ground controls and monitoring stations
User segment: Owned receivers
2.1 Space segment
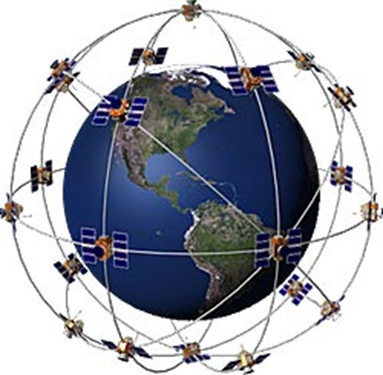
Constellation of 24 operational satellites
Run by the Department of Defense
- U.S. Air Force Space Command (AFSPC)
First satellite launched in 1978
Cost $10 billion
Triangulation-based technology
2.1.1 Operation
Fully operational on April 27, 1995
24 hours a day
All weather conditions
Orbit Earth every 12 hours
Altitude approximately at 20,200 km (12,600 nautical miles)
2.1.2 How many satellites?
Approximately 1,886!
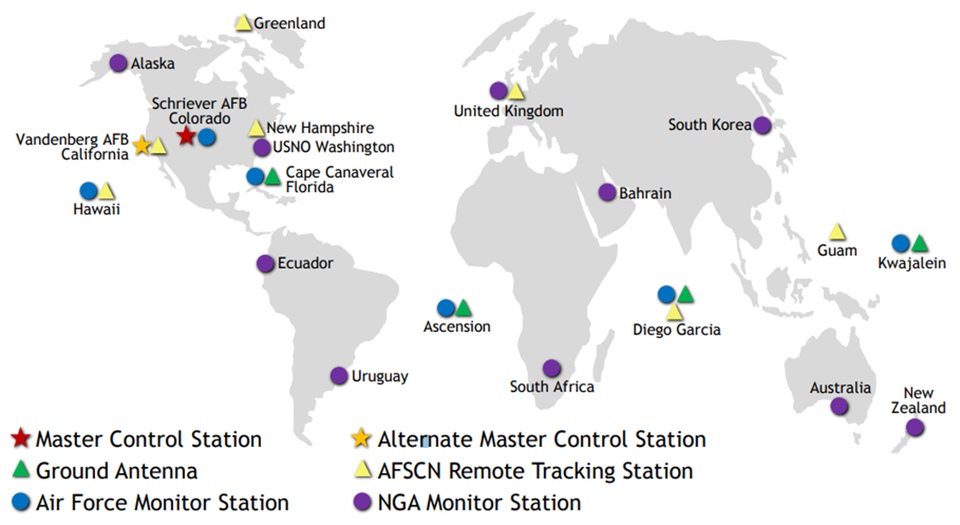
2.2 Control segment
- 1 master control station
- 1 alternate master control station
- 11 command and control antennas
- 16 monitoring sites
2.3 User segment
Your smartphone with a GPS!
Remember you have an inaccurate time.
3 How does it work?
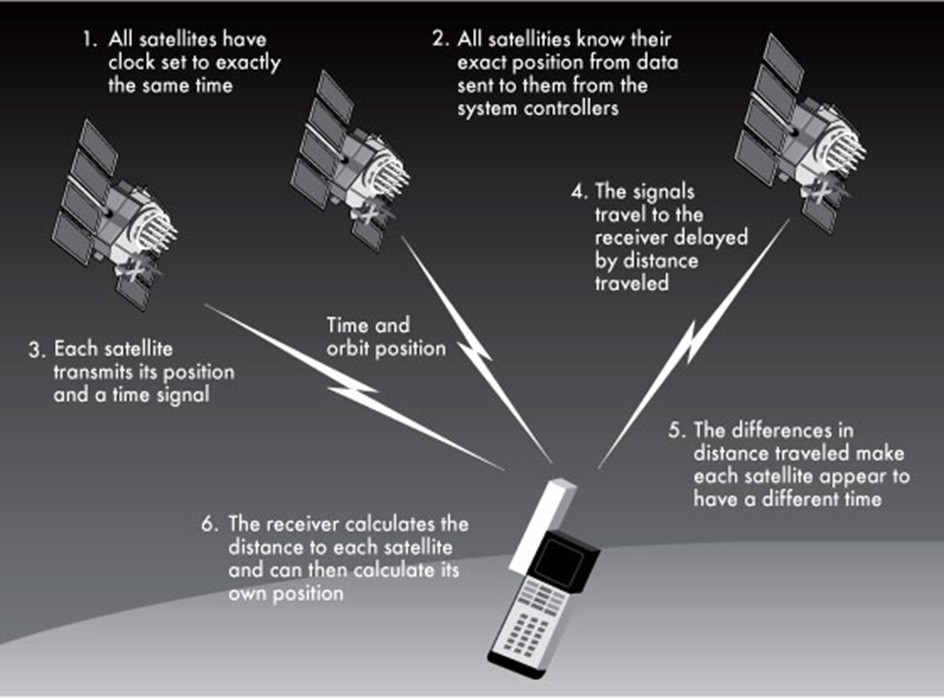
3.1 Five steps
Accurate timing
Satellite positioning
Satellite ranging
Trilateration
Error correction
3.1.1 Accurate timing
GPS determines its location by measuring time.
It ensures the accurate calculation of a distance.
Atomic clocks on GPS satellites are accurate to the nanosecond (10-9 second).
3.1.2 Satellite positioning
The satellites must know where themselves are.
Radars from ground stations constantly check each satellite to monitor changes in orbit.
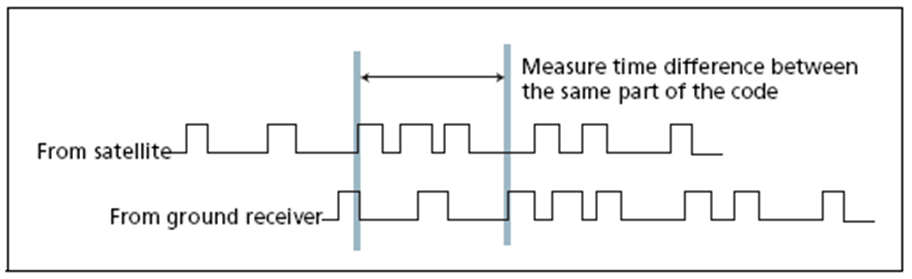
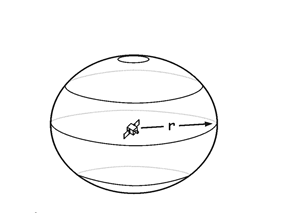
3.1.3 Satellite ranging
Measures the distance from the satellite to the receiver
\[ D=S\times T \]
- $D$: Distance between the satellite and receiver
- $S$: Speed of signal = 186,000 m/s in vacuum
- $T$: Time it takes for signal to be sent and received
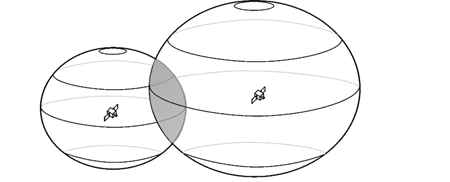
3.1.4 Trilateration
Basis of GPS
Measurements are made to calculate the distance from your location to a number of GPS satellites that are at different known locations.
Three variables
- How far is the point from the satellite?
- How long does it take for the radio signal to travel that distance?
- Where exactly are the satellites?
3.1.5 Error correction
$D=S\times T$ works only when $T$ is accurate.
Ideally, $T$ = GPS receiving time – Satellite sending time.
Satellite clocks are very accurate, but GPS clocks are not!
Now, $D=S\times T=S\times(\hat{T} + e)$
- $D$: Accurate distance
- $\hat{T}$: Inaccurate travel time
- $e$: Unknown constant error
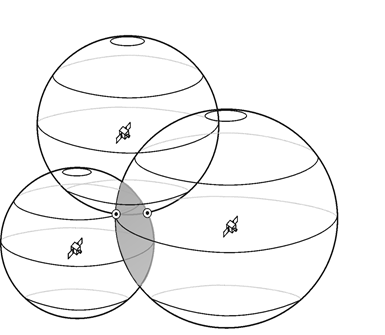
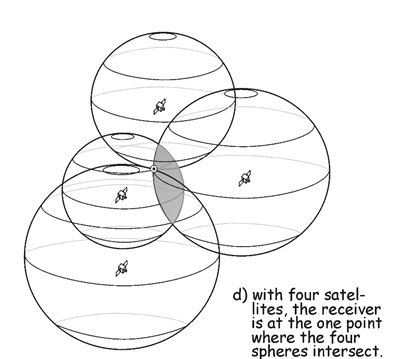
How many unknowns? $x$, $y$, $z$, and $e$ ⇒ We need four satellites!
3.2 System of equations
\begin{align*} (x-X_1)^2+(y-Y_1)^2+(z-Z_1)^2&=D(\hat{T}_1,e)^2\\ (x-X_2)^2+(y-Y_2)^2+(z-Z_2)^2&=D(\hat{T}_2,e)^2\\ (x-X_3)^2+(y-Y_3)^2+(z-Z_3)^2&=D(\hat{T}_3,e)^2\\ (x-X_4)^2+(y-Y_4)^2+(z-Z_4)^2&=D(\hat{T}_4,e)^2 \end{align*}
3.3 Why do we need four satellites again?
Why does GPS positioning require four satellites? Four unknown variables!
A typical misleading explanation