Momentum

1   Momentum equation review

\[ \newcommand{\volsym}{\rlap{\kern.08em–}V} \newcommand{\volsubsym}{\rlap{\scriptsize\kern.08em–}V} \] Momentum equation

We can use the momentum equation in open channel flow analysis when its complex internal flow patterns are unknown.

In steady flow, we ignore the control volume term because there is no change over time. \begin{equation} F_{p1}-F_{p2} =\rho Q(V_2-V_1) \end{equation} where $F_p$ is hydrostatic force and, 1 and 2 refer to the upstream and downstream sections, respectively.

If complex internal flow patterns are completely contained inside the control volume, flow analysis across the control surface becomes easier.

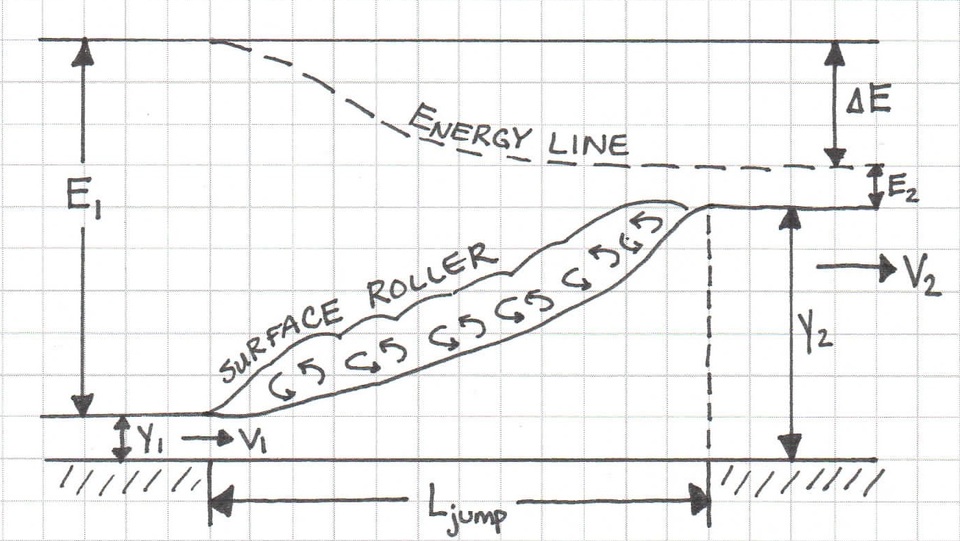
2   Hydraulic jump

See also Figure 3.1.

3   Momentum function

\begin{equation} F_{p1}-F_{p2} =\rho gh_{c1}A_1-\rho gh_{c2}A_2 =\rho Q(V_2-V_1) =\rho\frac{Q^2}{A_2-A_1} \end{equation} where $h_c$ is the centroidal depth.

\begin{equation} A_1h_{c1}+\frac{Q^2}{gA_1} =A_2h_{c2}+\frac{Q^2}{gA_2} \end{equation}

From this equality, we can define the momentum function

\begin{equation} M=Ah_c+\frac{Q^2}{gA} \end{equation}

Since $h_c$ is a unique function of the depth $y$ and the cross section geometry, we can use this function to determine the sequent depth before and after the jump given conditions at one section are given.

See Table 3.1.

4   Dimensionless analysis

See Figures 3.2–3.6.

5   Minimum value of the momentum function

For a rectangular channel, \begin{equation} \frac{M}{b}=\frac{y^2}{2}+\frac{q^2}{gy} \end{equation}

To find the minimum value of $M$, \begin{equation} \frac{d}{dy}\frac{M}{b}=y-\frac{q^2}{gy^2}=0 \end{equation}

$M$ becomes the minimum when \begin{equation} y=\left(\frac{q^2}{g}\right)^{1/3} \end{equation}

That equation looks very familiar. See Eq. (2.6) and Figure 3.9.

6   Exercise 3.1

Use Eqs. (2.21) and (3.4).

7   Homework: Exercise 3.2

Show your full work.

8   Stilling basins

9   Exercises

• Review Exercise 3.2
• Try Exercise 3.4
• Try Exercise 3.7
• Try Exercise 3.8

10   Surges

Surges are unsteady flows, but they can be analyzed in a stationary mannaer by superimposing the surge velocity $V_s$. See Figure 3.15.

11   Bridge piers

See Figure 3.16 and note $b=N_ps$ in the following derivation. \begin{equation} F_{p1}-F_{p4}-D=\rho\frac{Q^2}{A_4-A_1} \end{equation} Therefore, \begin{align} M_1&= M_4+\frac{D}{\gamma}\\ \frac{by_1^2}{2}+\frac{bq^2}{gy_1}&= \frac{by_4^2}{2}+\frac{bq^2}{gy_4}+\frac{C_D\rho A_pV_1^2}{2\rho g}\\ \frac{y_1^2}{2}+\frac{q^2}{gy_1}&= \frac{y_4^2}{2}+\frac{q^2}{gy_4}+\frac{C_DN_pay_1V_1^2}{2gN_ps}\\ \frac{y_1^2}{2}+\frac{q^2}{gy_1}&= \frac{y_4^2}{2}+\frac{q^2}{gy_4}+\frac{C_Day_1V_1^2}{2gs} \end{align} where $C_D$ is the drag coefficient, $a$ is the pier width, $s$ is the pier spacing, and $N_p$ is the number of piers.