Tags: ce 483, lectures, presentations

\[ \newcommand\si[1]{\mathrm{#1}} \newcommand\SI[2]{#1\,\si{#2}} \newcommand\matr[1]{\mathbf{#1}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \]

Hydrograph

CE 483

Dr. Huidae Cho

Department of Civil Engineering...New Mexico State University

Edit

Contents

1 Hydrograph time relationships
2 Travel time
3 Unit hydrograph
- 3.1 Example 9.1
- 3.2 Example 9.2
- 3.3 Example 9.3
4 S-hydrograph method
- 4.1 Example 9.4

1 Hydrograph time relationships

See Figure 9.8.

See TR-55: Urban Hydrology for Small Watersheds.

Flow over a watershed is a combination of sheet flow, shallow concentrated flow, and open channel flow.

Edit

2 Travel time

Edit

2.1 Sheet flow

Sheet flow is shallow flow with relatively a uniform depth, no longer than about 300 ft in natural watersheds.

\begin{equation} t_t=\frac{0.007(nL)^{0.8}}{P_2^{0.5}S^{0.4}} \end{equation}

$t_t$: Travel time (hr)
$n$: Manning’s roughness coefficient
$L$: Overland flow length (ft)
$P_2$: 2-year, 24-hour rainfall depth (in)
$S$: Slope of the surface (ft/ft)

Edit

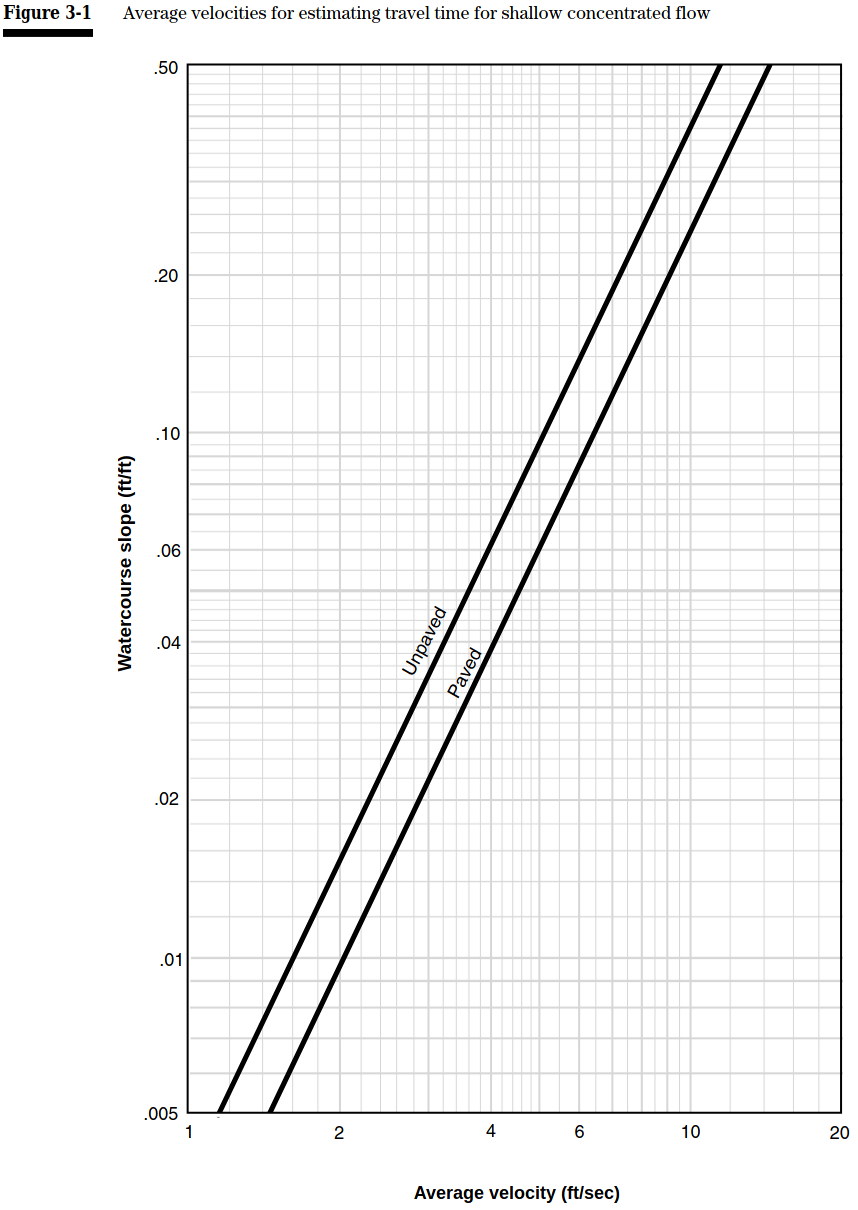
2.2 Shallow concentrated flow

Shallow concentrated flow usually occurs after a maximum of 300 ft of sheet flow before open channel flow forms.

Use Figure 3-1 in TR-55.

Edit

2.3 Open channel flow

Using Manning’s equation, \begin{equation} V=\frac{1.49}{n}R^{2/3}S^{1/2} \end{equation}

$V$: Average velocity (ft/s)
$n$: Manning’s roughness coefficient
$R=\frac{A}{P}$: Hydraulic radius (ft)
$A$: Flow area (ft²)
$P$: Wetted perimeter (ft)
$S$: Channel slope (ft/ft)

Edit

2.4 Exercise: Travel time

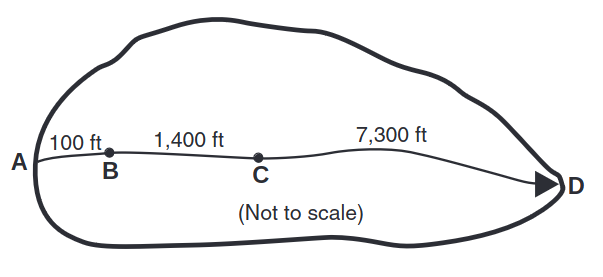
The figure below shows a watershed in Dyer County, northwestern Tennessee. Compute the time of concentration at the outlet of the watershed (point D). The 2-year, 24-hour rainfall depth is 3.6 in. Sheet flow occurs along segment AB (slope of 0.01, length of 100 ft, dense grass). Shallow concentrated flow occurs along segment BC (slope of 0.01, length of 1,400 ft, unpaved). Segment CD is an open channel (Manning’s roughness coefficient of 0.05, flow area of 27 ft², wetted perimeter of 28.2 ft, slope of 0.005, length of 7,300 ft).

Edit

3 Unit hydrograph

An “X-hour unit hydrograph” is a hydrograph derived from direct runoff from a storm event with a duration of X hours and a depth of 1 in (or cm).

See Figure 9.9.

Edit

3.1 Example 9.1

Using the total direct runoff hydrograph given in Table 9.3 columns (1)–(3), derive a unit hydrograph for the 1,715-ac drainage area.

Edit

3.2 Example 9.2

Discharge rates for the 2-hr unit hydrograph are

Time (hr)	0	1	2	3	4	5	6
Q (cfs)	0	100	250	200	100	50	0

Develop hourly ordinates of the total hydrograph resulting from a 4-hr design storm having the following excess amounts:

Time (hr)	1	2	3	4
Excess (in)	0.5	0.5	1.0	1.0

Edit

3.3 Example 9.3

Using the derived 2-hr unit hydrograph in Table 9.3, determine the direct runoff hydrograph for a 4-hr storm having the following excess rain amounts:

Time (hr)	1	2	3	4
Excess (in)	0.7	0.7	1.2	1.2

Edit

4 S-hydrograph method

See Figure 9.13.

Edit

4.1 Example 9.4

Given the following 2-hr unit hydrograph, use the S-hydrograph method to construct a 3-hr unit hydrograph.

Time (hr)	0	1	2	3	4	5	6
Flow (cfs)	0	100	250	200	100	50	0

Edit