\[ \newcommand\si[1]{\mathrm{#1}} \newcommand\SI[2]{#1\,\si{#2}} \newcommand\matr[1]{\mathbf{#1}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \]
Soil properties
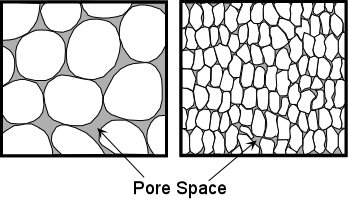
1 Porous medium
Soils are a porous medium because there are voids in the soil.
2 Porosity
Porosity ($\phi$) is calculated as the ratio of the volume of void ($V_v$) to the total soil volume ($V_t$) including the void.
\[\phi=\frac{V_v}{V_t}\]
For example, if the volume of void is $10\,\si{cm^3}$ and the total volume of a soil sample is $50\,\si{cm^3}$, voids take up 20% of the total volume.
3 Soil moisture content
When it rains, some of the water infiltrates into void spaces in the soil. This infiltration process forms groundwater when the infiltrated water reaches the water table. Partially or fully saturated soils lose their integrity and can be subject to a landslide depending on the slope and total weight of saturated soils.
It is our interest to measure how much water is in a soil sample.
3.1 Volumetric soil moisture content
\[\theta_v=\frac{V_w}{V_t}\] where $\theta_v$ is the volumetric soil moisture content, $V_w$ is the volume of water, and $V_t$ is the total soil volume including the volume of solids ($V_s$), of water ($V_w$), and of air ($V_a$).
3.2 Gravimetric soil moisture content
\[\theta_g=\frac{m_w}{m_s}\] where $\theta_g$ is the gravimetric soil moisture content, $m_w$ is the mass of water, and $m_s$ is the mass of solids.
4 Exercise: Gravimetric soil moisture content
You took a wet soil sample from the backyard. The mass of the sample was 370g. You let it completely dry out and measured its mass again. The dry mass is now 280g. What is the gravimetric soil moisture content?