Pipelines
Department of Civil and Environmental Engineering...New Mexico State University
Contents
1 What is pipe flow?
- No free surface (flow full)
- Driven by pressure head difference
- Analyzed using Darcy–Weisbach equation
1.1 Key distinction: Open channel vs pipe flow
| Open channel flow | Pipe flow |
|---|---|
| Free surface | No free surface |
| Driven by slope | Driven by pressure difference |
| Manning equation | Darcy–Weisbach equation |
2 Energy equation for pipe flow
General energy equation:
\[ \frac{P_1}{\gamma} + \frac{V_1^2}{2g} + z_1 - h_L = \frac{P_2}{\gamma} + \frac{V_2^2}{2g} + z_2 \]For constant diameter pipes ($V_1 = V_2$):
\[ h_L = \left(\frac{P_1}{\gamma} + z_1 \right) - \left(\frac{P_2}{\gamma} + z_2 \right) \]Key points:
- $h_L$ represents energy dissipation.
- Hydraulic grade line (HGL): $P/\gamma + z$
- Energy grade line (EGL): $P/\gamma + z + V^2/(2g)$
3 Head loss model
Major loss (friction):
\[ h_f = f \frac{L}{D} \frac{V^2}{2g} \]Minor loss:
\[ h_m = K \frac{V^2}{2g} \]Total head loss:
\[ h_L = h_f + \sum h_m \]4 Reynolds number
\[ Re = \frac{VD}{\nu} \]Flow regimes:
- Laminar: $Re < 2000$
- Transitional: $2000 \le Re \le 4000$
- Turbulent: $Re > 4000$
Question:
- What physical forces compete in $Re$?
5 Example 1: Laminar flow
Given:
- $\nu = 2.0 \times 10^{-4} \ \text{m}^2/\text{s}$
- $D = 0.05 \ \text{m}$
- $L = 20 \ \text{m}$
- $Q = 1.0 \times 10^{-4} \ \text{m}^3/\text{s}$
- Compute velocity:\[ V = \frac{Q}{\pi D^2/4} \]
- Compute Reynolds number:\[ Re = \frac{VD}{\nu} \]
- Determine regime
- If laminar, compute friction factor:\[ f = \frac{64}{Re} \]
- Compute head loss:\[ h_f = f \frac{L}{D} \frac{V^2}{2g} \]
Key points:
- No roughness required.
- Fully analytical solution.
6 Friction factor in turbulent flow
Colebrook equation:
\[ \frac{1}{\sqrt{f}} = -2 \log_{10} \left( \frac{\varepsilon}{3.7D} + \frac{2.51}{Re\sqrt{f}} \right) \]Key points:
- $f$ depends on $Re$.
- $f$ depends on relative roughness $\varepsilon/D$.
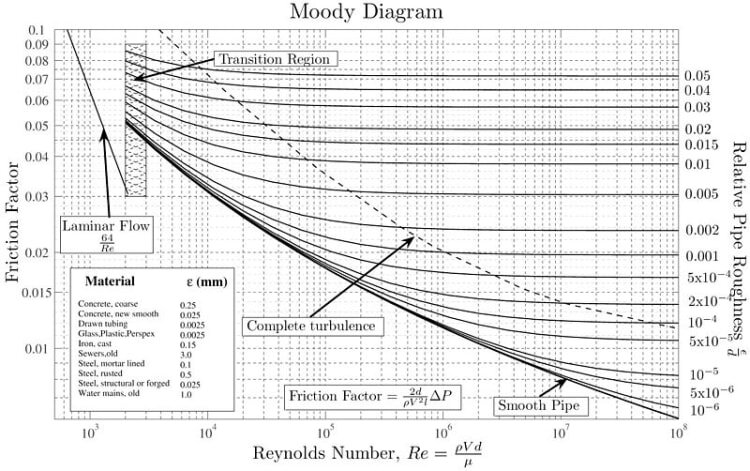
7 Moody diagram
Inputs:
- Reynolds number
- Relative roughness $\varepsilon/D$
Output:
- Friction factor $f$
Important regions:
- Laminar region
- Smooth pipe limit
- Fully rough region
8 Example 2: Turbulent flow
Given:
- $\nu = 1.0 \times 10^{-6} \ \text{m}^2/\text{s}$
- $D = 0.20 \ \text{m}$
- $L = 300 \ \text{m}$
- $Q = 0.05 \ \text{m}^3/\text{s}$
- $\varepsilon = 0.046 \ \text{mm}$
- Compute velocity:\[ V = \frac{Q}{\pi D^2/4} \]
- Compute Reynolds number:\[ Re = \frac{VD}{\nu} \]
- Compute relative roughness:\[ \frac{\varepsilon}{D} \]
- Read friction factor from Moody diagram
- Compute head loss:\[ h_f = f \frac{L}{D} \frac{V^2}{2g} \]
Key points:
- Roughness matters in turbulent flow.
- Follow the algorithm step by step.
9 Single pipe workflow
Remember:
- Compute velocity:\[ V = \frac{Q}{A} \]
- Compute Reynolds number:\[ Re = \frac{VD}{\nu} \]
- Determine regime
- Obtain friction factor $f$
- Compute head loss:\[ h_f = f \frac{L}{D} \frac{V^2}{2g} \]
If you remember this sequence, you can solve any single-pipe problem.
10 Pipe networks preview
Series condition:
\[ h_L = \sum h_{L,i} \]Parallel conditions:
\[ Q_T = Q_1 + Q_2 \] \[ h_{f,1} = h_{f,2} \]Next class:
- We solve network systems.