Digital image fundamentals
- 1 Principal energy source for digital images
- 2 Waves
- 3 Alternative energy sources
- 4 Imaging sensors
- 5 Digital image
- 6 Image sampling and quantization
- 7 Representation of digital images
- 8 Bits
- 9 Gray levels
- 10 Storage bits and bytes
- 11 Spatial and gray-level resolution
- 12 Homework: Wavelength and image storage
1 Principal energy source for digital images
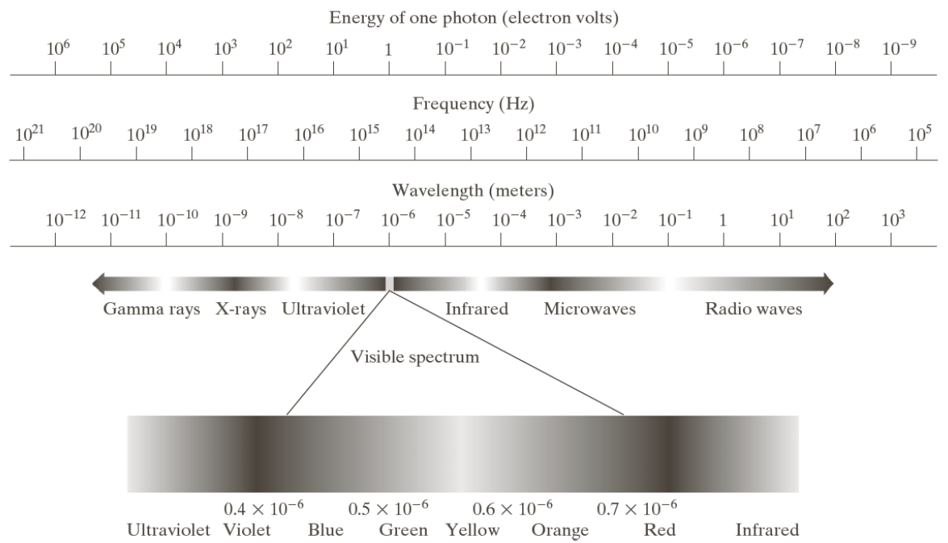
Principal energy source for images: Electromagnetic (EM) energy spectrum.
EM waves: Stream of massless particles (protons), each traveling in a wave-like pattern at the speed of light
Each massless particle has a bundle of energy called photon
2 Waves
Wavelength: $\lambda=\frac{c}{\nu}$
- $c$: Speed of light ($2.998\times 10^8 \mathrm{m/s}$)
- $\nu$: Frequency in Hz
- 1 Hz is 1 cycle of a sinusoidal wave per second
- Units of wavelength: m, microns ($\mathrm{\mu m}, 10^{-6} \mathrm{m}$), nanometers (nm, $10^{-9} \mathrm{m}$)
Energy: $E=h\nu$
- $h$: Planck’s constant ($4.135,667,66\times 10^{-15} \mathrm{eV}$)
- Units of energy: electron-volt (eV)
3 Alternative energy sources
Acoustic
- Geological applications: Mineral and oil exploration using low-frequency waves (e.g., 100 Hz)
- Low-frequency waves travel a longer distance because they lose less energy to the medium (less active $\rightarrow$ less loss)
Ultrasound
- Medical applications: Baby
- High-frequency waves (highly active $\rightarrow$ high loss)
Electronic
- Electron microscopy
4 Imaging sensors
5 Digital image
$f(x,y)=i(x,y)\times r(x,y)$
- $i(x,y) \in [0,\infty)$: Illumination, characteristics of the energy source
- $r(x,y) \in [0,1]$: Reflectance, characteristics of the object sensed
6 Image sampling and quantization
7 Representation of digital images
$M$ rows, $N$ columns
A digital image $=$ An $M$-by-$N$ matrix
By Python convention (because we use Python)
- Rows: $0,1,\cdots,M-1$
- Columns: $0,1,\cdots,N-1$
$f(x,y)=\begin{bmatrix} f(0,0)& \cdots& f(0,N-1)\\ \vdots& \ddots& \vdots\\ f(M-1,0)& \cdots& f(M-1,N-1) \end{bmatrix}$
$\mathbf{A}=\begin{bmatrix} a_{0,0}& \cdots& a_{0,N-1}\\ \vdots& \ddots& \vdots\\ a_{M-1,0}& \cdots& a_{M-1,N-1} \end{bmatrix}$
8 Bits
LSB: Least significant bit
MSB: Most significant bit
1 byte $=$ 8 bits
Unsigned integer $\in [2^0,2^8-1]=[0,255]$
What is this number in decimal notation?
9 Gray levels
Number of bits per pixel: $k$
Gray levels: $L=2^k$
$f(x,y)=\begin{cases} 0& \text{black}\\ L-1& \text{white} \end{cases}$
| $k$ | $L$ | Description |
|---|---|---|
| 1 | 2 | Binary image in black and white |
| 6 | 64 | 64 gray levels, limit of human visual system |
| 8 | 256 | Typical gray level resolution (1 byte per pixel) |
10 Storage bits and bytes
Storage bits: $b=M\times N\times k$
Storage bytes: $B=\left\lceil\frac{b}{8}\right\rceil$
Problems
- $M=N=32, L=2$
- $M=N=32, L=128$
11 Spatial and gray-level resolution
$M$ rows, $N$ columns, $L$ gray levels
Spatial resolution: $M\times N$ pixels, sometimes in pixels per inch (ppi)
Gray resolution: $L$ levels
Convention: $M\times N, L$-level image
For example,
- $512\times 512, 8$-level image
- $1024\times 1024, 256$-level image
12 Homework: Wavelength and image storage
- The frequency of commercial alternating current in the United States is 60 Hz. Find its wavelength.
- How many storage bits and bytes do you need to store a digital image of size 128-by-128 pixels and 256 gray levels?
Show your work for full credits!